前言

就是关于组合数的一些妙妙小式子。

有些名字是我自己取的，可能比较sb。

内容

杨辉三角

$$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$$

显然

递推式

$$ C_n^m=\frac{n}{m}C_{n-1}^{m-1}$$

显然

二项式定理

$$(a+b)^n=\sum_{i=0}^nC_n^ia^ib^{n-i}$$

归纳法可证

简单和

$$\sum_{i=0}^nC_n^i=2^n$$

二项式定理 $a=1,b=1$

交错和

$$\sum_{i=0}^n(-1)^iC_n^i=[n=0]$$

二项式定理 $a=1,b=-1$

带权和

$$\sum_{i=0}^nC_n^i*i=n*2^{n-1}$$

带进去算即可

$\sum_{i=0}^nC_n^i*i=\sum_{i=0}^n\frac{n!}{i!(n-i)!}i=\sum_{i=0}^n\frac{n!}{(i-1)!(n-i)!}=n\sum_{i=0}^n\frac{(n-1)!}{(i-1)!(n-i)!}=n\sum_{i=0}^nC_{n-1}^{i-1}=n*2^{n-1}$

$$\sum_{i=0}^nC_n^i*i^2=n*(n+1)*2^{n-2}$$

同理。为了方便，我直接跳步（

$\sum_{i=0}^nC_n^i*i^2=n\sum_{i=0}^nC_{n-1}^{i-1}*i=n\sum_{i=0}^{n-1}C_{n-1}^{i}*(i+1)=n\sum_{i=0}^{n-1}C_{n-1}^{i}*i+n\sum_{i=0}^{n-1}C_{n-1}^{i}=n*(n-1)*2^{n-2}+n*2^{n-1}=n*(n+1)*2^{n-2}$

如果你对 $\sum_{i=1}^nC_n^i*i^k$ 感兴趣的话。

竖向和

$$\sum_{i=0}^nC_i^m=C_{n+1}^{m+1}$$

考虑把杨辉三角画出来。

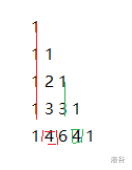
发现把顶上的那个 $1$，往右下挪一个，然后就像链条一样连起来了。

斜向和1

$$\sum_{i=0}^{n}C_{m+i}^i=C_{m+n+1}^{n}$$

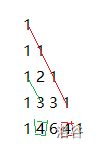
同理

合并1

$$C_n^mC_m^k=C_n^kC_{n-k}^{m-k}$$

考虑组合意义，左侧是 $n$ 个里面选了 $m$ 个球，然后这 $m$ 个球里选了 $k$ 个球，我们发现最后这 $k$ 个球构成的相同方案会被重复计数一些。

举个例子：$\{A,B,C,D,E\}$，$n=5,m=4,k=3$

第一步：$\{A,B,C,D\},\{A,B,C,E\},\{A,B,D,E\},\{A,C,D,E\},\{B,C,D,E\}$

第二步中，会出现两次 $\{A,B,C\}$。

右侧则是先直接在 $n$ 个里面选出那 $k$ 个球，然后考虑重复计数了几次。

这里计算重复计数的方法其实就是考虑一个大小为 $k$ 的集合被添加元素后成为若干个个大小为 $m$ 的集合的数量，这其实就是 $C_{n-k}^{m-k}$。

在刚刚的例子中，$C_{5-3}^{4-3}=2$，对应 $\{A,B,C,D\},\{A,B,C,E\}$ 这两个。

合并2

$$\sum_{i=0}^{k}C_n^{k-i}C_m^{i}=C_{n+m}^k$$

组合意义：相当于是先从 $n$ 个里面选出 $k-i$ 个，然后再在 $m$ 个中选择 $i$ 个，总共相当于在 $n+m$ 中选了 $k$ 个。

$$\sum_{i=0}^kC_k^nC_{k-i}^m=C_k^{n+m}$$

同理

斐波那契/斜向和2

$\sum_{i=0}^nC_{n-i}^i=Fib_{n+2}$

计算贡献，类似于刚刚的竖向和，但这玩意和斐波那契有关就让人感觉很 $6$。

总结

组合恒等式是很多的，或者不严格上地说是无限的。

一方面要根据题目实时变化，另一方面要明白组合恒等式背后的原理和思维，例如吸收公式、组合意义、代数推导等等。