【GDOI2008】彩球游戏colball

注意：本题解仅通过随机数据测试，请谨慎甄别 先讲讲题外话，这道题不管是从哪一方面都非常有思维难度。AI给出的难度评级为提高+/省选-，我认为应该为上位蓝或者下位紫，很难！真的很难！赛时最高分该题为10pts，这个出题人绝对是天才！也是猎奇了！
这里使用到了：双向广搜，哈希表，进制转换，状态压缩算法，请客观食用。

题面描述

Sarah 最近迷上了一个彩球游戏，游戏在一个 $N \times M$ 方格上分布有红、蓝、绿三种颜色的彩球，游戏者每次可以选中一个彩球，进行两种操作，如图 5.2.1 所示。(原图黑白不好理解，这里手绘展出，版权归 GDOI 所有，这里只做学术展示)
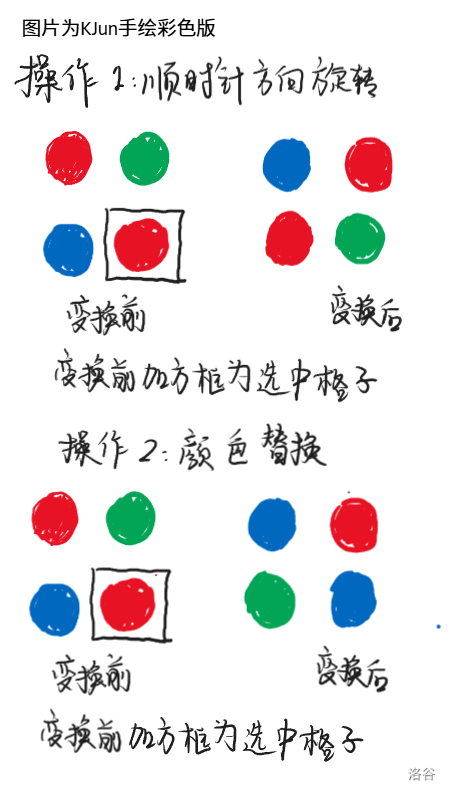
操作1：把以选中的球为右下角的四个相邻小球进行顺时针旋转。
操作2：把以选中的球为右下角的四个相邻小球进行颜色替换，替换规则为红色变蓝色，蓝色变绿色，绿色变红色。注意：每次操作都必须且仅能使用四个小球。这个游戏的目标是从给出的初始状态出发，用最少的操作达到目标状态。
输入格式输入不超过5组数据。 每组数据的第1行为 $N$ , $M$ 两个整数，输入 $N = 0$ 表示输入结束。然后 $N$ 行，每行是长度为 $M$ 的字符串，表示初始状态，用 RBG 代表红蓝绿三种颜色。然后 $N$ 行，每行是长度为 $M$ 的字符串，表示目标状态。输出格式对于每组数据，输出一个整数单独占一行，表示由初始状态到目标状态的最少操作次数，如果无解则输出 $-1$ 。
数据范围对于 $30\%$ 的数据，有 $2 \le N,M \le 4$, $ N \times M \le 9$ 。
对于 $50\%$ 的数据，有 $2 \le N,M \le 4$, $ N \times M \le 12$ 。
对于全部的数据，有 $2 \le N,M \le 4$, $ N \times M \le 16$ 。

思路解析

读题可知，我们希望在最大 $4 \times 4$ 的棋盘上维护换色和旋转操作，求出从初始状态到目标状态的最少步数，易得操作具有可逆性。
每一次操作都会影响后面的操作的初始状态，所以该题具有后效性，比较困难使用动态规划求解。 注意到 $N$ 和 $M$ 范围较小，所以考虑搜索解决该题。注意到可能有无解情况，所以不能死磕搜到头，不能使用 DFS 算法，应使用 BFS 算法。
考虑复杂度：每一个格子都有三种颜色，所以最多有 $3^{16}$ 个状态,大于 $4$ 千万。按照常理来说，这个时间跑现代评测机应该是压线很稳的，考虑到 2008 年的评测机器比较老旧，所以我们按照超时处理。
因为操作具有可逆性，所以考虑 Bidirectional BFS 算法（双向BFS）。从开始状态到目标状态进行搜索，直到两个队列有交集时，返回步数。枚举量最大为 $2 \times 3^{8}$，不管是老爷机还是中爷机统统跑过。
因为输入为字符串，不好操作而且不好判断交集，所以我们对棋盘进行编码（状态压缩/进制转换），方便操作。
具体优化细节看代码吧，挺多的。

完整代码？

#include <bits/stdc++.h>
#define inc(i, l, r) for(int i = l; i <= r; i++)
#define dec(i, l, r) for(int i = l; i >= r; i--)
using namespace std;
const int maxm = 43046721; // 3^16=43046721
int n, m;

// 因为有三钟颜色，所以使用三进制编码（确保状态唯一）
int encode(char sm[4][5]) {
    int ret = 0;
    inc(i, 0, n - 1) 
        inc(j, 0, m - 1) 
            ret = ret * 3 + sm[i][j];
    return ret;
}

// 三进制解码
void decode(int s, char sm[4][5]) {
    dec(i, n - 1, 0) dec(j, m - 1, 0) {
        sm[i][j] = s % 3;//取出最后一位放入格子
        s /= 3;//舍弃最后一位
    }
}

queue<int> que[2];          // 0:正向, 1:反向
unsigned char table[maxm];  // 记录步数
char vvv[maxm];             // 记录方向 (0/1/-1)

void insert(int v, int a, int b) { //记录步数与方向
    table[v] = b;
    vvv[v] = a;
}

// 颜色转换
void modify(char &p) {
    if (p == 'R') p = 0;
    else if (p == 'G') p = 1;
    else p = 2;
}

// 正向颜色变换：0->2, 1->0, 2->1
int change[3] = {2, 0, 1}; 
// 反向颜色变换：0->1, 1->2, 2->0
int restore[3] = {1, 2, 0}; 
//change 与 restore 操作互逆

int main() {
    freopen("colball.in", "r", stdin);
    freopen("colball.out", "w", stdout);
    
    while (scanf("%d", &n) == 1 && n) {//结束为 0 所以要判断一下
        scanf("%d", &m);
        char sm[4][5], tm[4][5], backup[4][5]; // backup用于完整状态备份

        // 读取初始状态
        inc(i, 0, n-1) {
            scanf("%s", sm[i]);
            inc(j, 0, m-1) modify(sm[i][j]);
        }
        // 读取目标状态
        inc(i, 0, n-1) {
            scanf("%s", tm[i]);
            inc(j, 0, m-1) modify(tm[i][j]);
        }

        // 检查相同状态
        int start_enc = encode(sm);
        int target_enc = encode(tm);
        if (start_enc == target_enc) {
            printf("0\n");
            continue;
        }

        // 初始化
        memset(vvv, -1, sizeof(vvv));
        memset(table, 0, sizeof(table));
        while (!que[0].empty()) que[0].pop();//防止数据污染 全部出队列
        while (!que[1].empty()) que[1].pop();
        
        que[0].push(start_enc);
        que[1].push(target_enc);//进队列
        insert(start_enc, 0, 0);
        insert(target_enc, 1, 0);//两个方向 步数为0

        int ans = -1;//默认无解
        bool found = false;

        while (!que[0].empty() && !que[1].empty() && !found) { //如果队列不为空（没搜完） 与 还没有搜到答案
            int p = (que[0].size() <= que[1].size()) ? 0 : 1; //优化1：平衡策略,选择探索范围小的进行拓展，防止陷入 dfs 的僵局
            int sz = que[p].size();
            
            while (sz-- && !found) { //如果队列不为空（没搜完） 与 当前轮次还没有搜到答案
                int cur = que[p].front(); que[p].pop();//取出队头
                int scur = table[cur];
                decode(cur, sm);//编码
                memcpy(backup, sm, sizeof(sm)); // 完整备份状态

                // 遍历所有2x2区域
                inc(i, 1, n-1) {
                    inc(j, 1, m-1) {
                        memcpy(sm, backup, sizeof(backup)); // 确保每次从原始状态开始
                        
                        // ========= 操作1：旋转 =========
                        int a = sm[i-1][j-1];
                        if (p == 0) { // 正向：顺时针
                            sm[i-1][j-1] = sm[i][j-1];
                            sm[i][j-1] = sm[i][j];
                            sm[i][j] = sm[i-1][j];
                            sm[i-1][j] = a;
                        } else { // 反向：逆时针
                            sm[i-1][j-1] = sm[i-1][j];
                            sm[i-1][j] = sm[i][j];
                            sm[i][j] = sm[i][j-1];
                            sm[i][j-1] = a;
                        }

                        // 计算新状态
                        int nxt = encode(sm);
                        int qv = vvv[nxt];
                        
                        if (qv == -1) { // 新状态
                            insert(nxt, p, scur + 1);
                            que[p].push(nxt);
                        } else if (qv != p) { // 双向相遇
                            ans = scur + table[nxt] + 1;//上面搜到的步数 + 下面搜到的步数 + 当前操作
                            found = true;
                            break;
                        }

                        // ========= 操作2：颜色变换 =========
                        memcpy(sm, backup, sizeof(backup)); // 恢复原始状态
                        inc(x, i - 1, i) inc(y, j - 1, j) 
                            sm[x][y] = (p == 0) ? change[sm[x][y]] : restore[sm[x][y]];
                        
                        nxt = encode(sm);
                        qv = vvv[nxt];
                        
                        if (qv == -1) {
                            insert(nxt, p, scur + 1);
                            que[p].push(nxt);
                        } else if (qv != p) {
                            ans = scur + table[nxt] + 1;
                            found = true;
                            break;
                        }
                    }
                    if (found) break;
                }
            }
        }
        printf("%d\n", found ? ans : -1);
    }
    return 0;
}